Tác giả: Martin Tingley với Wenjing Zheng, Simon Ejdemyr, Stephanie Lane, và Colin McFarland
Thuỳ biên dịch
Đây là bài thứ 3 trong loạt bài về cách Netflix ứng dụng A/B test để đưa ra quyết định và cải tiến sản phẩm.
Chúng ta có:
Phần 1: Quá Trình Ra Quyết Định Tại Netflix
Phần 2: Định Nghĩa A/B Test Của Netflix
Trong phần 2: Định Nghĩa A/B Test Của Netflix, chúng ta đã nói đến quá trình thử nghiệm cho tính năng Top 10 lists, và tham số được dùng làm thước đo chính để đưa ra quyết định là sự hài lòng của người xem đối với Netflix. Nếu một thử nghiệm như vậy cho thấy sự cải thiện đáng kể về mặt thống kê đối với chỉ số quyết định chính, thì tính năng này là một ứng cử viên đầy tiềm năng sẽ được triển khai cho toàn bộ người dùng. Nhưng làm thế nào để Netflix biết được khi nào họ đưa ra quyết định đúng dựa trên kết quả thử nghiệm? Điều quan trọng là phải hiểu rằng không có bất cứ phương pháp tiếp cận nào trong việc đưa ra quyết định có thể loại bỏ hoàn toàn những bấp bênh và khả năng mắc sai lầm. Sử dụng một khuôn khổ dựa trên việc hình thành giả thuyết, thực hiện A/B test, và phân tích thống kê cho phép Netflix định lượng những yếu tố bất định một cách cẩn thận, và biết được xác suất mắc phải những sai lầm khác nhau.
Có hai loại sai làm mà chúng ta có thể mắc phải khi xem xét kết quả thử nghiệm. Dương tính giả (hay còn được gọi là lỗi Loại I) xảy ra khi dữ liệu từ cuộc thử nghiệm cho thấy sự khác biệt có ý nghĩa giữa trải nghiệm của nhóm kiểm soát và nhóm nghiên cứu, nhưng sự thật là không có khác biệt nào. Tình huống này giống như là bạn làm xét nghiệm và nhận được kết quả dương tính đối với một loại bệnh nhưng thực chất là bạn hoàn toàn khỏe mạnh. Một lỗi khác mà chúng ta có thể mắc phải là âm tính giả (hay còn gọi là lỗi Loại II), xảy ra khi dữ liệu không chỉ ra sự khác biệt có ý nghĩa giữa trải nghiệm của nhóm kiểm soát và nhóm nghiên cứu, nhưng sự thật là có sự khác nhau. Tình huống này giống như là bạn làm xét nghiệm và nhận được kết quả âm tính – nhưng thực chất là bạn đã nhiễm bệnh.
Chúng ta cũng có thể diễn giải điều này theo một cách khác: Hãy coi lý do tồn tại của internet và machine learning chính là để gắn nhãn những bức ảnh có hình mèo trong đó. Đối với một bức ảnh, có hai quyết định có thể được đưa ra (bức ảnh được gắn nhãn là “mèo” hoặc “không có mèo”), và cũng tương tự như vậy, có hai sự thật có khả năng đúng (hình ảnh thực sự có mèo hoặc không). Điều này dẫn đến tổng cộng 4 kết quả có thể xảy ra, được cho thấy trong hình 1. Điều tương tự cũng xảy ra đối với A/B test: chúng ta đưa ra một hoặc hai quyết định dựa trên dữ liệu (“Có đủ bằng chứng để kết luận rằng Top 10 list ảnh hưởng đến sự hài lòng của người dùng” hoặc “Không đủ bằng chứng để kết luận), và có hai sự thật có thể là đúng, mà chúng ta không bao giờ biết được một cách chắc chắn (“Top 10 list thực sự ảnh hưởng đến sự hài lòng của người dùng” hoặc “Nó không có ảnh hưởng”).

Sự thật khó chịu về dương tính giả và âm tính giả là điều mà chúng ta không thể chối bỏ được, cũng không có cách gì để xử lý nó được. Trên thực tế, chúng đánh đổi chỗ cho nhau. Việc thiết kế thử nghiệm sao cho tỉ lệ khả năng xuất hiện dương tính giả là nhỏ nhất sẽ làm tăng tỉ lệ xuất hiện âm tính giả, và ngược lại. Trong thực tế, chúng ta cần hướng tới việc định lượng, hiểu và kiểm soát hai nguồn lỗi này.
Trong phần còn lại của bài này, chúng ta sẽ dùng các ví dụ đơn giản để làm rõ khái niệm dương tính giả và các khái niệm thống kê có liên quan. Và trong bài sau chúng ta sẽ nói đến âm tính giả.
Dương tính giả và ý nghĩa thống kê
Với một giả thuyết tuyệt vời và một hiểu biết rõ ràng về chỉ số quyết định chính, tiếp theo chúng ta tiếp tục xử lý các khía cạnh thống kê của việc thiết kế một A/B test. Quá trình này thường bắt đầu bằng cách xác định tỉ lệ dương tính giả châos nhận được. Theo quy ước, tỉ lệ dương tính giả thường được đặt ở mức 5%: đối với các thử nghiệm không chỉ ra được sự khác biệt có ý nghĩa nào giữa nhóm thử nghiệm và nhóm kiểm soát, chúng tôi sẽ có 5% khả năng kết luận sai rằng có sự khác biệt mang ý nghĩa thống kê. Các thử nghiệm được thực hiện với tỉ lệ dương tính giả là 5% được gọi là chạy ở mức ý nghĩa thống kê 5%.
Sử dụng quy ước mức ý nghĩa thống kê 5% có thể mang đến cảm giác không thoải mái. Khi tuân theo quy ước này, Netflix chấp nhận rằng trong trường hợp trải nghiệm của nhóm thử nghiệm và nhóm kiểm soát không có sự khác biệt có ý nghĩa đối với các thành viên, sẽ có 5% số lần họ mắc sai lầm. Họ sẽ đánh dấu 5% số ảnh không có mèo là “có mèo”.
Tỉ lệ dương tính giả có liên quan chặt chẽ đến “ý nghĩa thống kê” của những khác biệt có thể quan sát được trong các giá trị đo lường giữa nhóm thử nghiệm và nhóm kiểm soát, được đo bằng p-giá trị. p-giá trị là xác suất nhìn thấy một kết quả mang tính cực đoan ít nhất là bằng với kết quả của A/B test, nếu thực sự không có sự khác biệt nào giữa trải nghiệm của nhóm thử nghiệm và nhóm kiểm soát. Một cách trực quan để hiểu về ý nghĩa thống kê và p-giá trị, vốn là cách khái niệm khá rối ngay cả đối với các sinh viên thống kê trong hơn một thế kỷ qua (bao gồm cả tác giả bài viết này), là sử dụng ví dụ về các trò chơi may rủi đơn giản mà chúng ta có thể tính toán và hinh dung tất cả các xác suất có liên quan.

Ví dụ nếu chúng ta muốn biết là liệu đồng xu có fair hay không (hai mặt giống hệt nhau, hoặc khác nhau nhưng không làm ảnh hưởng đến xác suất xuất hiện của một trong hai mặt, hay có thể hiểu là xác suất xuất hiện một trong hai mặt bằng với xác suất xuất hiện của mặt kia khi gieo), theo nghĩa là số lần xuất hiện của mỗi mặt có đúng là 50% hay không. Đây có vẻ là một tình huống đơn giản, nhưng nó có liên quan đến rất nhiều doanh nghiệp, trong đó có Netflix, nơi mà mục tiêu là hiểu rõ liệu kết quả trải nghiệm sản phẩm mới có thể hiện ở một tỉ lệ khác đối với một số hoạt động của người dùng hay không, ví dụ như việc tiếp tục gia hạn sử dụng dịch vụ của Netflix. Vậy nên bất cứ hiểu biết nào có được thông qua những trò chơi đơn giản với đồng xu có thể được dùng trực tiếp để giải thích cho kết quả của A/B test.
Để xác định xem hai mặt của đồng xu có fair hay không, hãy chạy thử nghiệm sau: chúng ta sẽ tung đồng xu 100 lần, và tính toán tỉ lệ số lần xuất hiện mặt ngửa. Do sự ngẫu nhiên hoặc các yếu tố gây nhiễu, nên kể cả khi hai mặt của đồng xu hoàn toàn giống nhau thì chúng ta vẫn sẽ không thể có 50 lần sấp và 50 lần ngửa – nhưng độ lệch là bao nhiêu thì là “quá nhiều”? Khi nào thì chúng ta có đủ bằng chứng để bác bỏ khẳng định cơ bản là đồng xu này fair? Bạn có sẵn sàng kết luận khi có 60 lần xuất hiện mặt ngửa? 70? Chúng ta cần một cách để điều chỉnh dựa trên khung quyết định và hiểu về tỉ lệ dương tính giả liên quan.
Để hiểu rõ vấn đề này, hãy làm một bài tập tư duy. Đầu tiên, chúng ta sẽ giả định là đồng xu này fair – đây là “giả thuyết không” của chúng ta, vốn luôn là một tuyên bố về hiện trạng hoặc bình đẳng. Sau đó, chúng ta tìm kiếm bằng chứng thuyết phục chống lại giả thuyết này từ dữ liệu. Để đưa ra quyết định về việc đâu là bằng chứng thuyết phục, chúng ta tính toán xác suất của mọi kết quả có thể xảy ra, giả sử rằng giả thuyết không là đúng. Đối với ví dụ tung đồng xu, kết quả của 100 lần tung đồng xu là: lần 1 ngửa, lần 2 ngửa, lần 3 ngửa… cứ thế đến lần 100 ngửa – giả sử rằng đồng xu này fair. Chuyển sang phép toán, mỗi kết quả có thể xảy ra và xác suất liên quan của chúng được biểu thị bằng cách thanh màu đen và xanh lam trong hình 3. (Hãy tạm bỏ qua phần màu sắc)
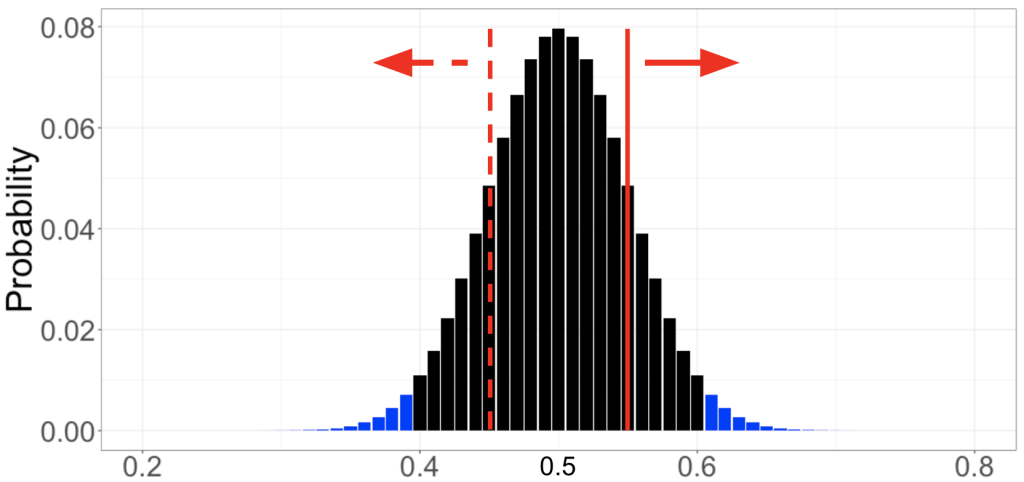
Chúng ta có thể so sánh phân phối xác suất này của các kết quả, được tính toán dựa trên giả định rằng đồng xu này fair, với dữ liệu mà chúng ta có được. Giả sử chúng ta thấy 55% trong số 100 lần tung đồng xu được mặt ngửa (đường liền nét màu đỏ trong hình 3). Để định lượng xem liệu quan sát này có phải là bằng chứng thuyết phục rằng đồng xu này fair hay không, chúng ta cần tính đến các xác suất liên quan đến các kết quả ít có khả năng xảy ra hơn. Ở đây, bởi vì chúng ta chưa đưa ra giả định nào về tỉ lệ xuất hiện của mặt ngửa và mặt sấp, chúng tôi tổng hợp xác suất 55% hoặc hơn số lần tung được mặt ngửa (các thanh bên phải của đường liền nét màu đỏ) và xác suất 55% hoặc hơn số lần tung được mặt sấp (các thanh bên trái đường đứt nét màu đỏ).
Đây là p-giá trị huyền thoại: xác suất nhìn thấy một kết quả cực đoan như quan sát của chúng ta, nếu giả thuyết không là đúng. Trong trường hợp của chúng ta, giả thuyết không là đồng xu này fair, quan sát là 55% xuất hiện mặt ngửa trên tổng số 100 lần tung, và p-giá trị ở khoảng 0.32. Chúng ta có thể giải thích như nhau: nếu chúng ta lặp lại vô số lần thí nghiệm tung đồng xu 100 lần và tính toán tỉ lệ xuất hiện mặt ngửa, với một đồng xu fair (giả thuyết không là đúng), 32% số lần thử nghiệm sẽ có kết quả là ít nhất 55% số lần xuất hiện mặt ngửa hoặc ít nhất 55% số lần xuất hiện mặt sấp.
Làm thế nào để sử dụng p-giá trị nhằm quyết định xem liệu có bằng chứng có ý nghĩa về mặt thống kê rằng đồng xu này không fair – hay trải nghiệm sản phẩm mới của Netflix giúp cải thiện sự hài lòng của khách hàng? Trở về với tỉ lệ dương tính giả 5% mà chúng ta đã đồng ý chấp nhận lúc đầu: chúng ta kết luận rằng có một ảnh hưởng mang ý nghĩa thống kê nếu p-giá trị nhỏ hơn 0.05. Điều này hình thức hoá trực giác của chúng ta rằng chúng ta nên bác bỏ giả thuyết không cho rằng đồng xu này fair nếu kết của của chúng ta ít khi xảy ra dưới giả định đồng xu này fair. Trong ví dụ trên, chúng ta quan sát thấy 55 trong số 100 lần tung đồng xu xuất hiện mặt ngửa, chúng ta tính toán được p-giá trị là 0.32. Vì p-giá trị lớn hơn mức ý nghĩa thống kê 0.05, chúng ta kết luận rằng không có bằng chứng có ý nghĩa thống kê cho thấy rằng đồng xu này không fair.
Có hai kết luận có thể rút ra từ một thử nghiệm hoặc A/B test: chúng tôi kết luận là có ảnh hưởng (“đồng xu này fair”, “Tính năng Top 10 giúp tăng sự hài lòng của người dùng”) hoặc chúng tôi kết luận rằng không có đủ bằng chứng để kết luận là có ảnh hưởng (“không thể kết luận rằng đồng xu này không fair”, “không thể kết luận là tính năng Top 10 giúp gia tăng sự hài lòng của người dùng”). Nó rất giống với bồi thẩm đoàn ở toà, có hai kết luận có khả năng được đưa ra: “có tội” hoặc “không có tội” – và “không có tội” không có nghĩa là “trong sạch”. Tương tự như vậy, cách tiếp cận này (frequentist) đối với AB test không cho phép chúng ta đưa ra kết luận là không có ảnh hưởng – chúng ta không bao giờ kết luận là đồng xu này fair, hay tính năng mới của sản phẩm không hề có tác động gì đến người dùng. Chúng ta chỉ kết luận rằng không đủ bằng chứng để bác bỏ giả thuyết không rằng không có sự khác biệt nào cả. Trong ví dụ về đồng xu ở trên, chúng ta nhận thấy có 55 lần xuất hiện mặt ngửa trong tổng số 100 lần tung đồng xu, và kết luận rằng chúng ta không đủ bằng chứng để bác bỏ giả thuyết không rằng đồng xu này fair. Quan trọng là, chúng ta không kết luận rằng hai đồng xu này fair – sau cùng, nếu chúng ta có thể thu thập thêm bằng chứng, ví dụ như tung đồng xu đó 1000 lần, chúng ta có thể tìm thấy đủ bằng chứng thuyết phục để bác bỏ giả thuyết không.
Miền bác bỏ và Miền tin cậy
Có hai khái niệm khác trong A/B test có liên quan chặt chẽ đến p-giá trị: miền bác bỏ của một thử nghiệm, và miền chấp thuận của một quan sát. Chúng ta sẽ nói đến cả hai trong phần này, dựa trên ví dụ về đồng xu ở trên.
Miền bác bỏ. Một cách khác để xây dựng một quy tắc ra quyết định cho một thử nghiệm là dựa trên cái gọi là “miền bác bỏ” – một bộ giá trị trong đó chúng ta có thể kết luận rằng đồng xu này không fair. Để tính toán miền bác bỏ, chúng ta một lần nữa giả định rằng giả thuyết không là đúng (đồng xu này fair), và sau đó xác định miền bác bỏ là tập hợp các kết quả có ít khả năng xảy ra nhất với tổng xác suất không lớn hơn 0.05. Miền bác bỏ bao gồm các kết quả cực đoan nhất, với điều kiện giả thuyết không chính xác – các kết quả cho thấy bằng chứng chống lại giả thuyết không mạnh mẽ nhất. Nếu một quan sát rơi vào miền bác bỏ, chúng ta kết luận rằng có bằng chứng có ý nghĩa về mặt thống kê cho thấy đồng xu này không fair, và “bác bỏ” giả thuyết không. Trong trường hợp của thí nghiệm đồng xu, miền bác bỏ tương ứng với việc kết quả cho thấy có ít hơn 40% hoặc nhiều hơn 60% số lần xuất hiện mặt ngửa (các thanh màu xanh trong Hình 3). Chúng ta gọi các ranh giới của miền bác bỏ, ở đây là ít hơn 40% hoặc nhiều hơn 60% số lần xuất hiện mặt ngửa là các giá trị quan trọng của thí nghiệm.
Có sự tương đương giữa miền bác bỏ và p-giá trị, và cả hai đều dẫn đến cùng một quyết định: p-giá trị nhỏ hơn 0.05 chỉ khi kết quả thu được nằm trong miền bác bỏ.
Miền tin cậy. Đến hiện tại, chúng ta đã tiếp cận cách xây dựng quy tắc quyết định bắt đầu với giả thuyết không, vốn luôn là một tuyên bố không thay đổi hoặc tương đương (“đồng xu này fair” hay “tính năng mới của sản phẩm không ảnh hưởng đến sự hài lòng của người dùng”). Sau đó chúng ta xác định các kết quả có thể xảy ra dưới giả thuyết không này và so sánh quan sát/kết quả thực nghiệm của chúng ta với bảng phân phối đó. Để hiểu về miền tin cậy, hãy tập trung vào kết quả thực nghiệm. Sau đó chúng ta sẽ thực hiện một số bài tập tư duy: với kết quả thực nghiệm mà chúng ta thu được, các giá trị nào của giả thuyết không sẽ dẫn đến quyết định không bác bỏ, giả sử chúng ta chỉ định tỉ lệ dương tính giả là 5%? Đối với ví dụ tung đồng xu của chúng ta, kết quả thu được là 55% trên tổng số 100 lần tung đồng xu xuất hiện mặt ngửa và chúng ta không bác bỏ giả thuyết không rằng đồng xu này fair. Chúng ta cũng không bác bỏ giả thuyết không nếu xác suất xuất hiện mặt ngửa là 47.5%, 50% hay 60%. Có một loạt các giá trị mà chúng ta sẽ không bác bỏ giả thuyết không, từ 45% đến 65% số lần xuất hiện mặt ngửa (Hình 4).
Phạm vi giá trị này là miền tin cậy: tập hợp các giá trị trong giả thuyết không dẫn đến việc việc bác bỏ, dựa trên dữ liệu thực nghiệm. Bởi vì chúng ta đã vạch ra miền này bằng cách dùng các thử nghiệm ở mức ý nghĩa thống kê 5%, chúng ta đã tạo một miền tin cậy ở mức 95%. Có thể hiểu rằng, dưới các thử nghiệm lặp đi lặp lại, 95% số lần thực nghiệm có giá trị thực (ở đây là xác suất xuất hiện mặt ngửa) rơi vào miền tin cậy .
Có sự tương quan giữa miền tin cậy và p-giá trị, và cả hai đều dẫn đến cùng một quyết định: 95% miền tin cậy không chứa giá trị không khi và chỉ khi p giá trị nhỏ hơn 0.05, và cả hai trường hợp chúng ta bác bỏ giả thuyết không không có hiệu lực.
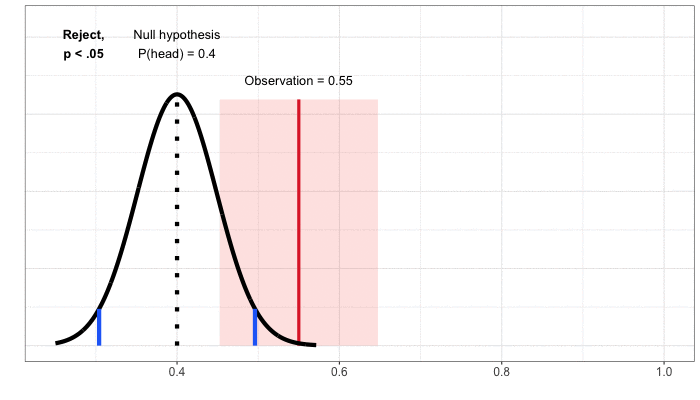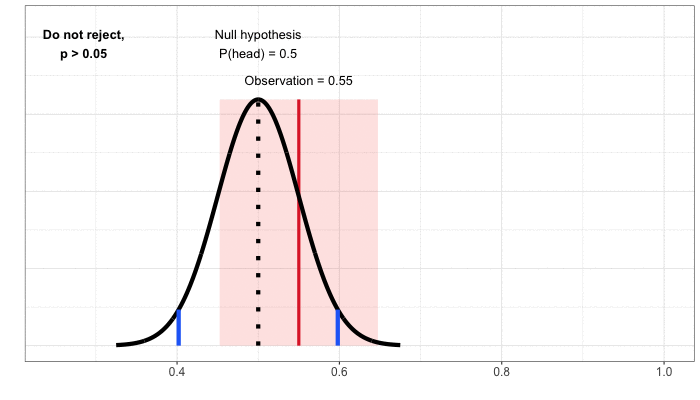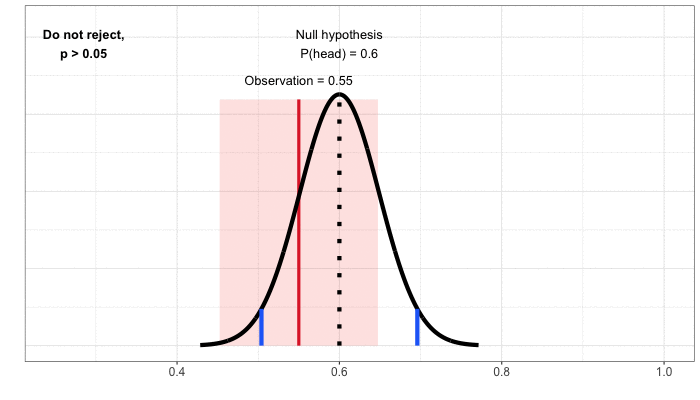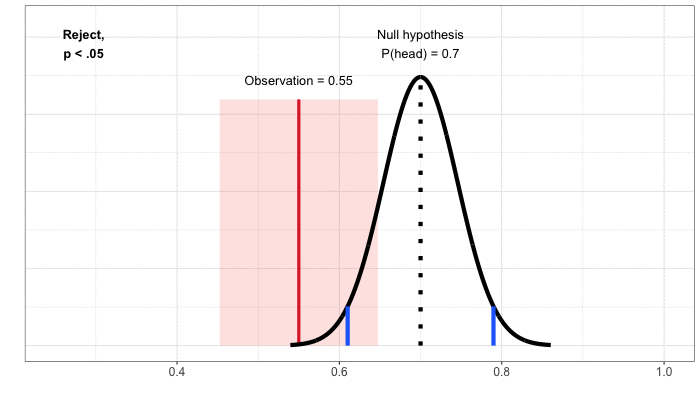
Hình 4: Xây dựng miền tin cậy bằng cách lập bản đồ giá trị, khi được sử dụng để xác định giả thuyết không, sẽ không dẫn đến việc bác bỏ một quan sát nhất định.
Kết luận
Sử dụng một chuỗi bài tập tư duy dựa trên thí nghiệm tung đồng xu, chúng ta đã hiểu về dương tính giả, ý nghĩa thống kê và p-giá trị, miền bác bỏ, miền tin cậy và hai quyết định mà chúng ta có thể đưa ra dựa trên dữ liệu thực nghiệm. Đây là các khái niệm căn bản và kiến thức này có liên quan trực tiếp đến việc so sánh trải nghiệm của nhóm thử nghiệm và nhóm kiểm soát trong A/B test. Chúng ta xác định một “giả thuyết không” không có sự khác biệt: trải nghiệm “B” không làm thay đổi đổi sự hài lòng của người dùng. Sau đó chúng ta sử dụng cùng một thử nghiệm tư duy: đâu là các khả năng có thể xảy ra và xác suất tương ứng của chúng đối với sự khác biệt trong các giá trị đo lường giữa nhóm thử nghiệm và nhóm kiểm soát, giả sử không có sự khác biệt trong sự hài lòng của người dùng? Sau đó chúng ta có thể so sánh kết quả của thử nghiệm với phân phối này, hệt như trong ví dụ về đồng xu, tính một p-giá trị và đưa ra kết luận về cuộc thử nghiệm. Và cũng giống như ví dụ đồng xu, chúng ta có thể xác định miền bác bỏ và và tính toán miền tin cậy.
Nhưng dương tính giả không phải là lỗi duy nhất trong số hai lỗi mà chúng ta có thể mắc phải trong quá trình xem xét kết quả thử nghiệm. Trong bài tới, chúng ta sẽ cùng tìm hiểu về lỗi thứ hai, âm tính giả, và các khái niệm có liên quan chặt chẽ đến sức mạnh thống kê. Các bạn có thể follow blog của mình để được cập nhật về bài viết mới.


Bình luận về bài viết này