Tác giả: Martin Tingley with Wenjing Zheng, Simon Ejdemyr, Stephanie Lane, và Colin McFarland
Thuỳ biên dịch

Đây là phần thứ tư trong series nhiều tập về cách Netflix sử dụng A/B test để hỗ trợ ra quyết định và cải tiến chất lượng sản phẩm.

Đọc thêm:

Phần 1: Quá Trình Ra Quyết Định Tại Netflix

Phần 2: Định Nghĩa A/B Test Của Netflix

Phần 3: Cách Netflix Diễn Giải Kết Quả A/B test: Dương Tính Giả Và Ý Nghĩa Thống Kê

Trong phần trước, chúng ta đã xác định hai loại sai lầm có thể xảy ra khi giải thích kết quả thử nghiệm: dương tính giả và âm tính giả. Sau đó chúng ta đã dùng một bài tập tư duy đơn giản dựa trên ví dụ tung đồng xu để hiểu về dương tính giả và các khái niệm liên quan ví dụ như ý nghĩ thống kê, p giá trị và khoảng tin cậy. Trong bài này, chúng ta sẽ làm điều tương tự để tìm hiểu về âm tính giả và các khái niệm có liên quan đến sức mạnh thống kê (statistical power, hay SP) – xác suất bác bỏ giả thuyết không khi giả thuyết này là sai .

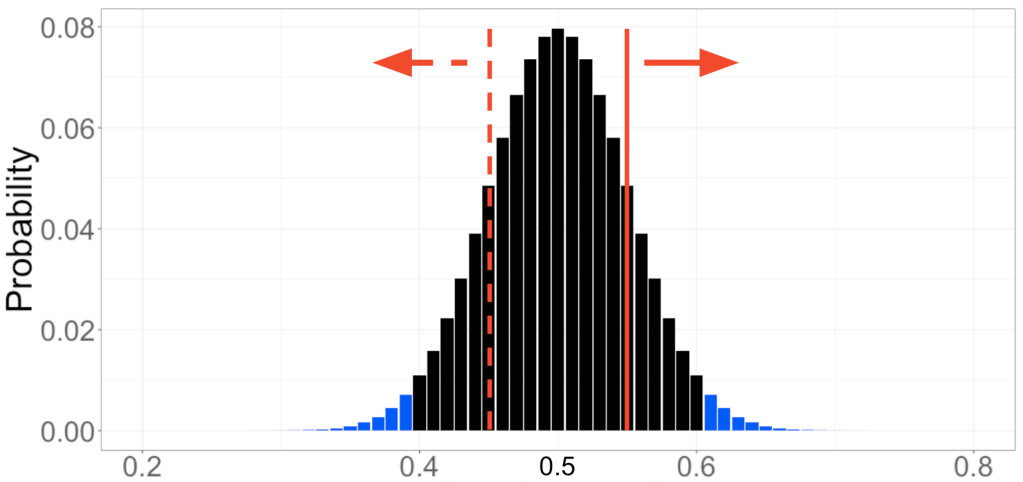
Hình 1: Cũng như trong phần 3, chúng ta sẽ dùng các bài tập tư duy dựa trên ví dụ tung đồng xu để hiểu về các khái niệm quan trọng của thống kê.

Âm tính giả và sức mạnh thống kê

m tính giả diễn ra khi dữ liệu không chỉ ra sự khác biệt có ý nghĩa giữa nhóm kiểm soát và nhóm nghiên cứu, nhưng thực tế lại có khác biệt. Tiếp tục sử dụng ví dụ mà chúng ta đã dùng trong phần 3, âm tính giả tương ứng với việc gắn nhãn bức hình con mèo là “không phải mèo”. m tính giả có liên quan chặt chẽ đến một khái niệm thống kê là ‘sức mạnh thống kê’ (statistical power), cho xác suất về kết quả dương tính thực sự dựa trên thử nghiệm và hệ số ảnh hưởng thực sự. Trên thực tế, sức mạnh thống kê là một trừ cho tỉ lệ âm tính giả.

Sức mạnh thống kê liên quan đến việc xem xét các kết quả có thể xảy ra dựa trên giả định cụ thể về trạng thái thực tế của thế giới – tương tự như cách chúng ta định nghĩa ý nghĩa thống kê bằng cách, trước tiên giả định giả thuyết không là đúng trong Phần 3. Để hiểu thêm về sức mạnh thống kê, hãy quay lại ví dụ về đồng xu giống như trong Phần 3, ở đây mục tiêu là quyết định xem liệu hai mặt của đồng xu có giống hệt nhau hay không bằng cách sử dụng một thí nghiệm tính tỷ lệ mặt ngửa xuất hiện trong 100 lần tung. Phân phối (distribution) các kết quả theo giả thuyết không rằng hai mặt của đồng xu là giống nhau được thể hiện bằng đường màu đen trong Hình 2. Để làm cho biểu đồ dễ hiểu hơn, chúng tôi đã làm mịn phần trên cùng của các biểu đồ.

Điều gì sẽ xảy ra trong thí nghiệm này nếu hai mặt của đồng xu không giống nhau? Để giúp cho bài tập tưởng tượng này cụ thể hơn, hãy giả sử chúng ta có một đồng xu mà khi tung, tần suất xuất hiện mặt ngửa trung bình là 64% (lý do chúng tôi chọn con số này sẽ được giải thích sau). Bởi vì có sự không chắc chắn hoặc nhiễu trong thí nghiệm của chúng tôi, chúng tôi không mong đợi thấy chính xác 64 mặt ngửa trong 100 lần tung. Nhưng giống như giả thuyết không đặt ra rằng đồng xu có hai mặt giống nhau, chúng tôi có thể tính toán tất cả các kết quả có thể xảy ra nếu giả thuyết thay thế này là đúng. Phân phối này được thể hiện bằng đường cong màu đỏ trong Hình 2.

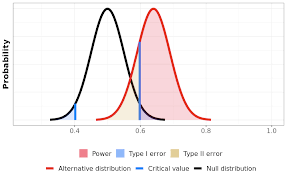
Hình 2: Minh họa sức mạnh thống kê bằng ví dụ tung một đồng xu 100 lần và tính tỷ lệ mặt ngửa. Các đường nét đứt màu đen và đỏ lần lượt cho thấy phân phối các kết quả giả định xác suất mặt ngửa là 50% (giả thuyết không) và 64% (giá trị cụ thể của giả thuyết thay thế). Ở đây, sức mạnh thống kê chống lại giả thuyết thay thế này là 80% (phần bóng màu đỏ).

Về mặt hình ảnh, sức mạnh thống kê là phần của phân phối thay thế (màu đỏ) nằm ngoài các giá trị quan trọng theo giả thuyết không (các đường màu xanh và đường cong màu đen; xem Phần 3). Ở đây, 80% phân phối thay thế (màu đỏ) rơi vào phía bên phải của đường màu xanh cao hơn, đánh dấu giá trị quan trọng của vùng từ chối trên. Giả sử rằng đồng xu này thực sự có xác suất xuất hiện mặt ngửa là 64%, thì sức mạnh thống kê của bài kiểm tra này là 80%. Cũng có một phần nhỏ không đáng kể của phân phối thay thế (màu đỏ) rơi vào vùng từ chối dưới (ở phía bên trái của đường màu xanh ngắn).

Sức mạnh thống kê của một thử nghiệm tương ứng với hệ số ảnh hưởng được giả định cụ thể. Trong ví dụ của chúng ta, thử nghiệm có sức mạnh thống kê là 80% để phát hiện rằng một đồng xu có hai mặt không đều nhau, nếu đồng xu đó thực sự có xác suất mặt ngửa bằng 64%. Cách giải thích như sau: nếu đồng xu có xác suất mặt ngửa bằng 64%, và chúng ta lặp lại thí nghiệm tung đồng xu đó 100 lần và đưa ra quyết định ở mức ý nghĩa 5%, thì chúng ta sẽ từ chối giả thuyết không rằng đồng xu có hai mặt đều nhau trong khoảng 4 trong mỗi 5 thí nghiệm. Và 20% của những thí nghiệm lặp lại đó sẽ dẫn đến kết quả âm tính giả: chúng ta sẽ không bác bỏ giả thuyết không rằng đồng xu có hai mặt đều nhau, mặc dù hai mặt của nó thực chất không đều nhau.

Cách tăng sức mạnh thống kê

Khi thiết kế A/B test, trước tiên chúng ta chọn chọn mức ý nghĩa thống kê (quy ước là 5%: nếu không có sự khác biệt giữa nhóm kiểm soát và nhóm nghiên cứu, chúng ta sẽ thấy dương tính giả xuất hiện khoảng 5%), và sau đó thiết kế thử nghiệm để kiểm soát âm tính giả. Có ba đòn bẩy chính mà chúng ta có thể sử dụng để tăng sức mạnh thống kê và giảm xác suất âm tính giả:
Hệ số ảnh hưởng. Nói một cách đơn giản, hệ số ảnh hưởng càng lớn – sự khác biệt về chỉ số đo lường giữa hai nhóm A và B – xác suất mà chúng ta có thể phát hiện chính xác sự khác biệt đó càng cao. Để hiểu một cách trực quan, hãy sử dụng thí nghiệm để xác định xem hai mặt của một đồng xu có đều nhau hay không, trong đó dữ liệu chúng tôi thu thập là tỷ lệ mặt ngửa trong 100 lần tung. Tưởng tượng rằng có hai kịch bản có thể xảy ra. Trong kịch bản đầu tiên, xác suất xuất hiện mặt ngửa là 55%, và trong kịch bản thứ hai, con số này là 75%. Theo trực giác (và toán học) thì rất có thể xác định kết quả thí nghiệm là hai mặt của đồng xu không đều nhau trong kịch bản thứ hai. Xác suất xuất hiện mặt ngửa cao hơn nhiều so với trị không 50%, vì vậy rất có thể rằng thí nghiệm sẽ tạo ra một kết quả rơi vào vùng từ chối. Trong bối cảnh phát triển sản phẩm, chúng ta có thể tăng mức độ biến động số liệu dự kiến bằng cách táo bạo hơn, thay cho việc kiểm tra giả thuyết theo cách tích lũy. Một chiến lược khác để tăng hệ số ảnh hưởng là thử nghiệm trong các khu vực mới của sản phẩm, nơi có thể có nhiều không gian hơn để cải thiện sự hài lòng của người xem. Tuy nhiên, một trong những niềm vui của việc thực hiện các thử nghiệm là yếu tố bất ngờ: đôi khi, những thay đổi dường như nhỏ có thể có tác động lớn đến các chỉ số hàng đầu.

Kích thước mẫu. Kích thước mẫu càng lớn, sức mạnh thống kê càng cao và việc xác xác định các hiệu ứng nhỏ hơn càng dễ dàng. Để hiểu một cách trực quan, hãy tiếp tục lấy ví dụ về thí nghiệm xác định xem liệu hai mặt của một đồng xu có đều nhau hay không. Ở đây, dữ liệu chúng tôi thu thập là tỷ lệ mặt ngửa trong một số lần tung cố định và xác suất xuất hiện mặt ngửa là 64%. Xem xét hai kịch bản sau: trường hợp đầu tiên, chúng ta tung đồng xu 20 lần, và trong trường hợp thứ hai, chúng ta tung đồng xu 100 lần. Theo trực giác (và toán học), rất có thể thí nghiệm của chúng ta xác định đồng xu có hai mặt không đều nhau trong kịch bản thứ hai. Với nhiều dữ liệu hơn, kết quả từ thí nghiệm sẽ gần với tỷ lệ thực sự của 64% mặt ngửa, trong khi giả định rằng đồng xu này có hai mặt đều nhau theo lý thuyết sẽ cho kết quả thực tế vào khoảng 0,50, khiến vùng từ chối vượt 50% giá trị. Những hiệu ứng này kết hợp lại với nhau, vì vậy với nhiều dữ liệu hơn, xác suất kết quả từ thí nghiệm với đồng xu sẽ rơi vào vùng từ chối lớn hơn, dẫn đến một kết quả dương tính đúng. Trong ngữ cảnh phát triển sản phẩm, chúng ta có thể tăng sức mạnh thống kê bằng cách phân bổ thêm số thành viên (hoặc các đơn vị khác) vào thử nghiệm hoặc giảm số lượng nhóm thử nghiệm, mặc dù có sự đánh đổi giữa kích thước mẫu trong mỗi thử nghiệm và số lượng thử nghiệm không chồng chéo có thể được chạy cùng một lúc.

Sự biến đổi của số liệu trong quần thể cơ bản. Số liệu trong quần thể mà chúng ta thử nghiệm càng đồng nhất thì việc xác định chính xác hiệu ứng thực sự càng dễ dàng. Vấn đề này hơi khó hình dung một chút, và các ví dụ đơn giản về đồng xu cuối cùng cũng không còn phù hợp. Giả sử tại Netflix rằng chúng tôi chạy một thử nghiệm nhằm giảm một số tham số đo lường về độ trễ, chẳng hạn như độ trễ giữa việc một thành viên nhấn phát và việc phát lại video bắt đầu. Do sự đa dạng của các thiết bị và kết nối internet mà mọi người sử dụng để truy cập Netflix, có rất nhiều biến động tự nhiên trong chỉ số này này giữa các người dùng khác nhau. Do đó, nếu giải pháp thử nghiệm dẫn đến việc chỉ số độ trễ giảm đi một chút, thì cũng không dễ để có thể xác định liệu giải pháp này có thực sự hiệu quả hay không – “nhiễu” từ sự đa dạng của chỉ số này làm cho tín hiệu nhỏ bị át đi. Ngược lại, nếu chúng tôi chạy thử nghiệm trên một tập hợp các thành viên sử dụng các thiết bị tương tự với các kết nối web tương tự, thì tín hiệu nhỏ dễ dàng xác định hơn – có ít nhiễu gây ảnh hưởng đến tín hiệu hơn. Tại Netflix, chúng tôi dành rất nhiều thời gian để xây dựng các mô hình phân tích thống kê tận dụng kiến thức này, và tăng sức mạnh thống kê bằng cách giảm biến thiên một cách hiệu quả; xem ở đây để biết mô tả kỹ thuật về cách tiếp cận của chúng tôi.

Sức mạnh thống kê cho các hiệu ứng hợp lý và có ý nghĩa

Sức mạnh thống kê và tỷ lệ âm tính giả là các hàm của hệ số ảnh hưởng giả định. Giống như việc tỷ lệ dương tính giả 5% là một quy ước được chấp nhận rộng rãi, sức mạnh thống kê 80% cho hệ số ảnh hưởng hợp lý và có ý nghĩa cũng được sử dụng rộng rãi (chúng tôi sẽ đề cập đến các thuật ngữ này dưới đây). Đó là, chúng tôi giả định một hệ số ảnh hưởng và sau đó thiết kế thử nghiệm, chủ yếu thông qua việc thiết lập kích thước mẫu, sao cho, nếu tác động thực sự của thử nghiệm là như chúng tôi đã giả định, thử nghiệm sẽ có độ chính xác là 80%. Và 20% kết quả từ thử nghiệm sẽ là âm tính giả: thực tế, có một hiệu ứng, nhưng quan sát của chúng tôi từ thử nghiệm không nằm trong vùng từ chối và chúng tôi không kết luận rằng có một hiệu ứng. Đó là lý do tại sao các ví dụ ở trên sử dụng xác suất 64% mặt ngửa: một thí nghiệm với 100 lần tung sau đó có sức mạnh thống kê 80%.

Việc xác định hệ số ảnh hưởng hợp lý có thể khó khăn, vì các thử nghiệm có thể làm chúng ta ngạc nhiên. Nhưng sự kết hợp của kiến thức về ngành mà chúng ta đang làm việc và các hiểu biết chung về toán và thống kê thường cho phép chúng ta ước lượng chính xác. Trong một lĩnh vực mà việc thử nghiệm đã được sử dụng từ lâu để tối ưu hóa các hệ thống đề xuất giúp các thành viên Netflix chọn nội dung phù hợp nhất với họ, chúng tôi biết rõ hệ số ảnh hưởng mà các thử nghiệm của chúng tôi thường tạo ra (dù là dương tính hay âm tính). Với sự hiểu biết về hệ số ảnh hưởng trong các thử nghiệm ở quá khứ, cũng như chiến lược phân tích, chúng tôi có thể thiết lập kích thước mẫu để đảm bảo rằng bài kiểm tra có sức mạnh thống kê là 80% cho một sự biến thiên số liệu hợp lý.

Điều thứ hai cần xem xét, cả trong giai đoạn thiết kế thử nghiệm và trong việc quyết định nên đầu tư nỗ lực của mình vào đâu, là xác định điều gì tạo thành tác động có ý nghĩa đối với các chỉ số chính được sử dụng để quyết định kết quả thử nghiệm. Điều gì là có ý nghĩa sẽ phụ thuộc vào lĩnh vực tác động của thử nghiệm (sự hài lòng của thành viên, độ trễ phát lại, hiệu suất kỹ thuật của hệ thống back end, v.v.), và có thể là nỗ lực hoặc chi phí liên quan đến trải nghiệm sản phẩm mới. Giả sử, nếu hệ số ảnh hưởng nhỏ hơn 0,1% thay đổi trong chỉ số chính, thì chi phí hỗ trợ tính năng sản phẩm mới vượt quá lợi ích. Trong trường hợp này, không có nhiều ý nghĩa khi tăng sức mạnh thống kê của một thử nghiệm để phát hiện 0,01% thay đổi trong chỉ số, vì việc xác định thành công một hiệu ứng có kích thước đó sẽ không dẫn đến sự thay đổi có ý nghĩa trong quyết định. Tương tự, nếu hệ số ảnh hưởng được thấy trong các thử nghiệm trong một lĩnh vực đổi mới nhất định là không liên quan đến trải nghiệm người dùng hoặc doanh nghiệp, đó là dấu hiệu rằng nguồn lực thử nghiệm có thể được triển khai hiệu quả hơn ở nơi khác.

Kết luận

Phần 3 và 4 của loạt bài này tập trung vào việc định nghĩa và giải thích một cách trực quan về các khái niệm cốt lõi được sử dụng để phân tích kết quả kiểm tra: dương tính giả và âm tính giả, ý nghĩa thống kê, giá trị p và sức mạnh thống kê.

Một sự thật khó chịu về thử nghiệm là chúng ta không thể cùng lúc giảm thiểu cả âm tính giả và dương tính giả. Thực tế, dương tính giả và âm tính giả đánh đổi với nhau. Nếu chúng ta sử dụng tỷ lệ dương tính giả nghiêm ngặt hơn, chẳng hạn như 0,01%, chúng ta sẽ giảm tỉ lệ dương tính giả cho các thử nghiệm nơi không có sự khác biệt giữa A và B – nhưng chúng ta cũng sẽ giảm sức mạnh thống kê của thử nghiệm đó vì tỉ lệ âm tính giả sẽ tăng, cho những thử nghiệm có sự khác biệt có ý nghĩa. Sử dụng tỷ lệ dương tính giả 5% và nhắm đến sức mạnh thống kê 80% là những quy ước được thiết lập tốt, cân nhắc giữa việc hạn chế phát hiện sai và tăng tỉ lệ phát hiện đúng. Tuy nhiên, trong các trường hợp mà dương tính giả (hoặc âm tính giả) gây ra rủi ro lớn hơn, các nhà nghiên cứu có thể không tuân thủ các quy tắc này này để giảm thiểu một trong hai khả năng sai.

Mục tiêu của chúng tôi không phải là loại bỏ sự không chắc chắn, mà là hiểu và định lượng sự không chắc chắn để đưa ra quyết định chính xác. Trong nhiều trường hợp, kết quả từ A/B test đòi hỏi sự giải thích tinh tế, và thực tế kết quả thử nghiệm chỉ là một đầu trong số nhiều yếu tố ảnh hưởng đến quyết định kinh doanh. Trong bài viết tiếp theo, chúng ta sẽ đề cập đến cách xây dựng sự tự tin khi đưa ra quyết định bằng cách sử dụng kết quả thử nghiệm.